Big-Theta Notation : Theory and Calculation

Before reading this notes, I recommend you to read following articles:

1. Big-Oh : In Layman's terms
2. Big-Oh : Theory & Calculation
3. Big-Omega : Theory & Calculation

---

You can have both lower bound and upper bound on a function.

If and then,
is sandwiched between and ,
If , we say
It's read as is Big-Theta of .

Big-Theta Notation ()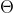

Definition: = { if and only if = and = for all }

• i.e., is the set of function that are in both and for all . Thus, we have an asymptotic tight bound on the running time. "Asymptotic" because it's paramount only for large values of n. "Tight bound" because the running time is nailed within a constant factor above (upper bound) and below (lower bound).

• It is used to compare 'run-time' or growth rate between two growth functions.

• Another method to determine the condition: 

 , where  , if such  c does exist then

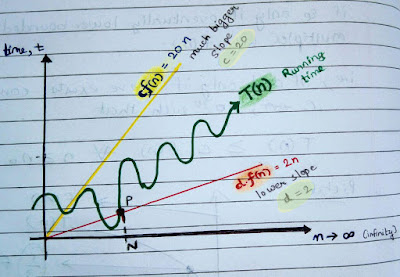Fig. 1: Time-complexity : Graph to illustrate the concept of Big-Theta Notation

Explanation:

•  If we have any function which fits between lower linear line  and upper linear line as then, that function is in .

  

• In Fig. 1, initially, the graph T(n) is not between the lower and upper bound. But, after a while its' always between the lower and upper bound. So, this function is said to be in .

Note: If . 

Example:- 

When we say that a particular running time is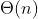 we mean to say that once T(n) gets large enough, the running time is at least 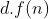and at most .

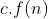Imagine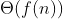 :- (Observe 'Fig. 1' while reading this): For some trivial values of 'n' we ignore how the graph looks, but after the value of 'n' gets large enough (i.e., for n>N) i.e., on the R.H.S of the vertical line PN, the running time must be sandwiched between the asymptotic lower bound ( 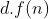) and upper bound (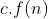).  As long as the constant d and c exist we say that the running time is .

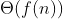Remember following rules while solving for Big-Theta Notation:

1. For any two functions, , if and are both bounded as 'n' grows to infinity, then In that case, is both an upper bound and a lower bound on the growth of .   
2. By definition for a function to be in Big-Theta(some function), it has to be both in asymptotic lower (Big-Omega notation) and upper bound (Big-Oh notation). So, check for both these conditions separately. 

Now let's solve some questions:

---

Q.1. Does ?

Sol.  No, , because 'n' is not an asymptotic upper bound for .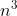

---

Q.2. Does  ?

Sol. No, because 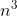 is not an asymptotic lower bound on 'n'.

Therefore, .

---

Note: 

• Interpret Big-Oh notation carefully. For instance, if I say an algorithm  , it's not guaranteed that the algorithm runs "slow". As, it could also mean that it run in O(n) time. We can also say that it runs in time. Therefore, big-oh notation can be misleading. BUT big-theta notation can't be misleading. So, if I say your algorithm , it really is slow. 

• Finally, all these asymptotic notations (Big-Oh, Big-Omega, and Big-Theta) are always independent of what function you are representing. So, Big-Oh doesn't always mean worst-case running time. Big-Omega doesn't always mean best-case running time.You always have to ask what function is being bounded when you use these notations.

• You can always derive Big-Oh and Big-Omega from Big-Theta by is definition.

• It is of paramount importance that one must not confuse the bound with the case. A bound (like Big-Oh, Big-Omega, Big-Theta) - says something about the rate of growth. A case says something about the kinds of input you're currently considering to be processed by your algorithm.

---

Refresh capsule:

1. (Big-Oh) means that the growth rate of is asymptotically less than or equal to to the growth rate of .
2. (Big-Omega) means that the growth rate of is asymptotically greater than or equal to the growth rate of .
3. (small-oh) means that the growth rate of is asymptotically less than the growth rate of .
4. (small-omega) means that the growth rate of is asymptotically greater than the growth rate of .
5. (Big-Theta) means that the growth rate of is asymptotically equal to the growth rate of